负数取模运算的一点小探究

起因

事情是这样的，在执行下面这段代码的时候会得到下面的结果。

// Main.java
class Main {
    public static void main(String[] args) {
        System.out.println(-9 % 2);
        System.out.println(-9 % -2);
        System.out.println(9 % -2);
        System.out.println(9 % 2);
    }
}
// Output:
-1
-1
1
1

我就奇了怪了，这负数取余是咋算的，怎么结果还带负数的。顺手抓了 JavaScript 和 python 两个脚本语言去试了试。

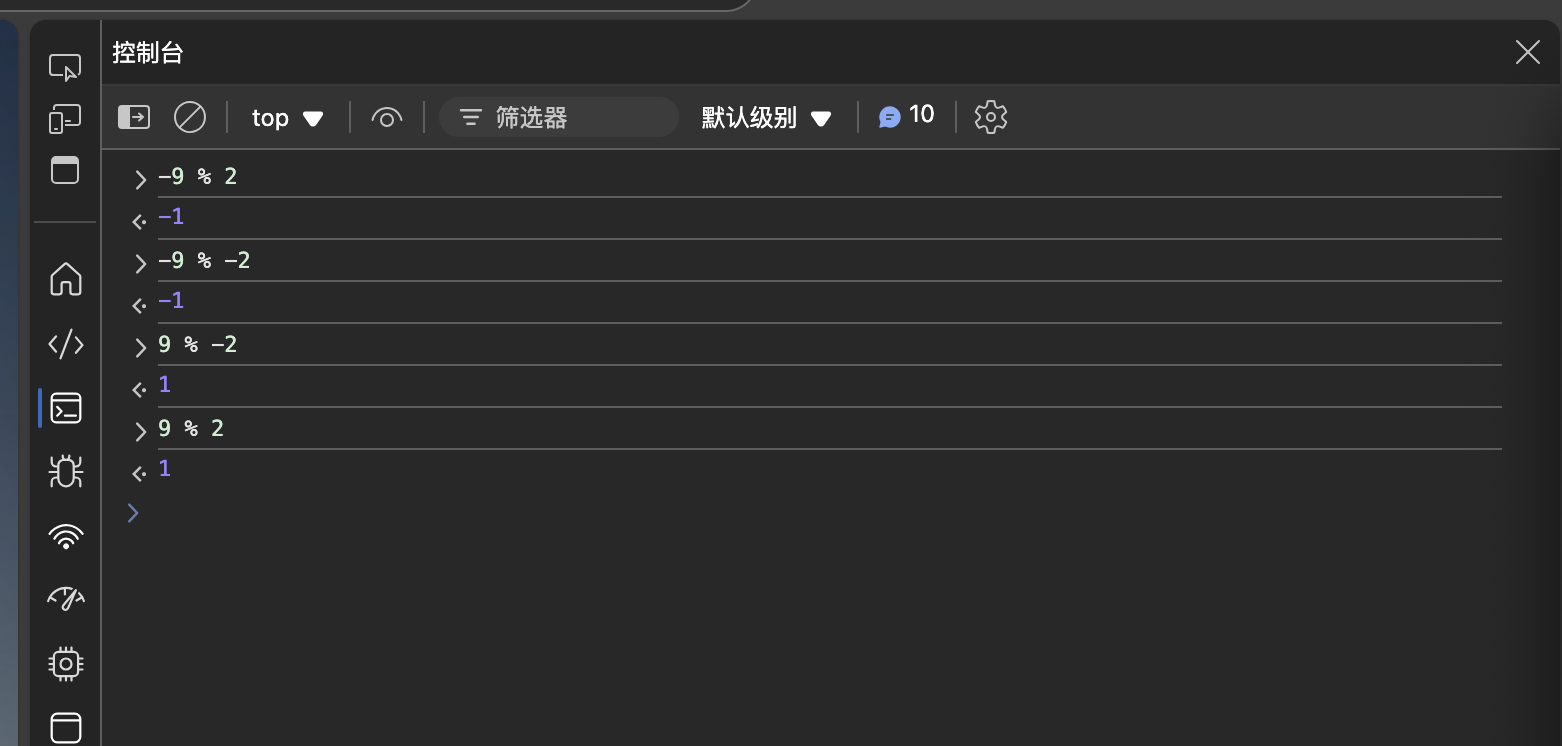
javascript取模结果

JavaScript 的结果（上图）跟 java 是一致的，就在我以为这可能是某种知识盲区里的约定时，python 的结果却显得格外特立独行（下图）。

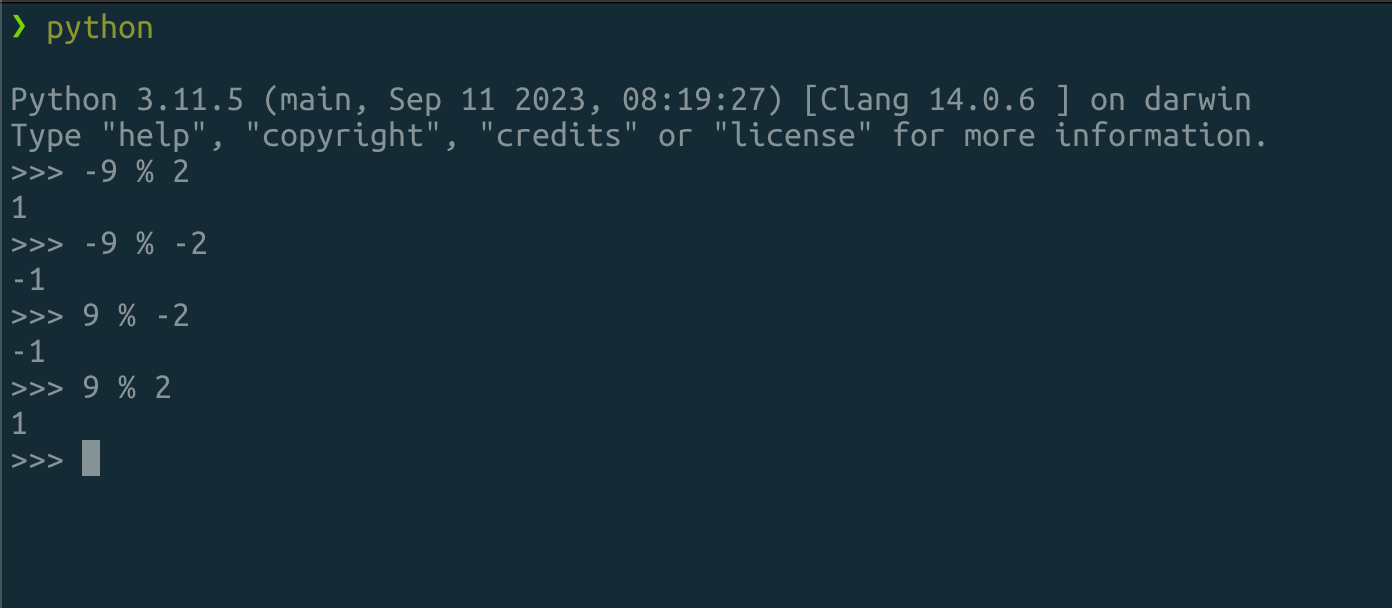
python取模结果

事情变得吊诡起来，也就是说，并没有一种约定限制负数域的取模操作应该是怎样的结果。这就会导致跨语言开发者不仅要防备着语法的串味，就连这种看上去完全相同的操作符 %，也需要保持着对结果不一致的预期，慎之又慎。

要想搞明白这一切，就得扒开 % 操作符底层的真实计算过程。而后才知道它什么时候会是负数，取值范围如何，结果的分布如何等等一系列问题的答案，在进行代码编写的时候做到心中有数。

比如伪代码：randomInt() % n 通常被我们拿来取随机值，那么这个随机值的范围便不再是[0,n)。假设 randomInt() 能做到均匀分布，那么取模之后的结果是否依旧还是均匀分布呢。

又比如 m % n 通常被拿来算哈希，分桶。假设一排哈希桶用一个数组装起来，我们直接拿着结果作为下标去索引，就很容易被负数域干扰从而数组越界。

甚至用 n % 2 == 1 来判断 -9 是不是奇数在 java 和 JavaScript 中都不能如愿。

这些问题在没有搞清楚具体实现之前，都得打上一些问号。

那么以 java 为例，来探究一下取模操作 % 究竟在干什么！

取模操作在 java 中的实现

首先，写一段简单的 java 代码。里面仅包含一个静态方法main(String...)作为入口函数,以及一个静态方法mod(int, int)用于取模运算。不用上面的代码，单独定义一个函数，防止为了提高效率，编译的时候直接把运算结果作为常数塞进去输出，没有体现取模的过程。

// Main.java
class Main {
    public static void main(String[] args) {
    }
    public static int mod(int a, int b) {
        return a % b;
    }
}

我们都知道，java、kotlin 程序是基于 jvm 运行的。具体来说是将 java 代码转换成 jvm 认识的平台无关的字节码（由 jvm 规范定义的一套指令集组成），然后在 jvm 上解释执行每条指令（当然还有 jit，在此不做过多讨论），以此来屏蔽不同架构、操作系统的实现和指令集的差异，从而实现传说中的一次编写，各处运行。这一特性为 java 当年的风靡提供了不小的助力。而像 c/c++、golang 这些编程语言，则需要将代码编译成具体目标平台的可执行文件（其中包含了数据和该平台上支持的机器指令），若是想支持多个平台，那么就得编译成多份可执行文件。虽然支持交叉编译，但一份代码在不同环境下的分发和部署得进行多次编译，管理和维护也显得比较麻烦。

像 docker 这种的容器化玩法，借助 cgroups 和 namespace 相关的技术，在一定程度上保障了容器间资源和权限的隔离。使用定义式的镜像，将运行环境也一并打包了进去，使得无论在开发过程中的个人电脑上还是在生产环境的服务器端，都能得到一致的程序运行环境保障。而其分层的镜像结构设计，使得打包过程也不至于过慢（反倒是防火墙有时会拖后腿）。随着互联网应用和互联网用户的大爆发，微服务架构得到普及，容器化方案以其一致性和隔离性的保障，加之快速构建和部署的能力，以及对资源使用的明确预期，得到了大范围的应用。加之 k8s 这类容器编排平台的出现以及云原生生态的成长，调度、管理、功能等各方面都有了极高的灵活型。日志、监控、调度、缩扩容等大多数场景在 CNCF 项目中都能找到较为成熟的解决方案。这是现状，但即使这样，回到最根本的镜像，也还是得去适配不同的 cpu 架构（为不同的架构打不同的镜像）。

作为一个意识流玩家，不小心扯远了。

既然 java 代码的执行需要转换成字节码，接下来我们就得看看这个取模方法的字节码究竟长什么样，都执行了哪些步骤。进入到 Main.java 所在的目录，执行如下命令：

❯ javac Main.java && javap -c Main                                           
Compiled from "Main.java"
class Main {
  Main();
    Code:
       0: aload_0
       1: invokespecial #1                  // Method java/lang/Object."<init>":()V
       4: return

  public static void main(java.lang.String[]);
    Code:
       0: return

  public static int mod(int, int);
    Code:
       0: iload_0
       1: iload_1
       2: irem
       3: ireturn
}

其中 javac 将代码编译为字节码文件（你的当前目录下将出现一个Main.class），然后 javap -c 反编译该字节码文件并将其字节码指令显示出来。

关注到 mod 方法部分，熟悉汇编的朋友们一眼应该就知道它肚子里憋的什么屁。这里还是翻译一下，第一步是将第一个操作数放到操作数栈的最顶上，第二步是将第二个操作数放到操作数栈的最顶上，第三步把上面两个操作数拿出来进行运算，算出来的结果放回操作数栈，最后一步把栈顶的操作数作为返回值返回。其前缀 i 大概率指的就是对 int 的操作。

emmm，没有解答我的疑问啊，还得再往下挖。现在最关键的就是搞清楚这个 irem 到底做了些什么。既然这玩意是 jvm 规定的，且由 jvm 去执行。那么就有两个简单朴素的思路，一个是看他怎么规定的，一个是去看他怎么执行的。

找到 oracle 对 java 字节码操作指令的定义，其中有这这样一部分的定义^[1]：

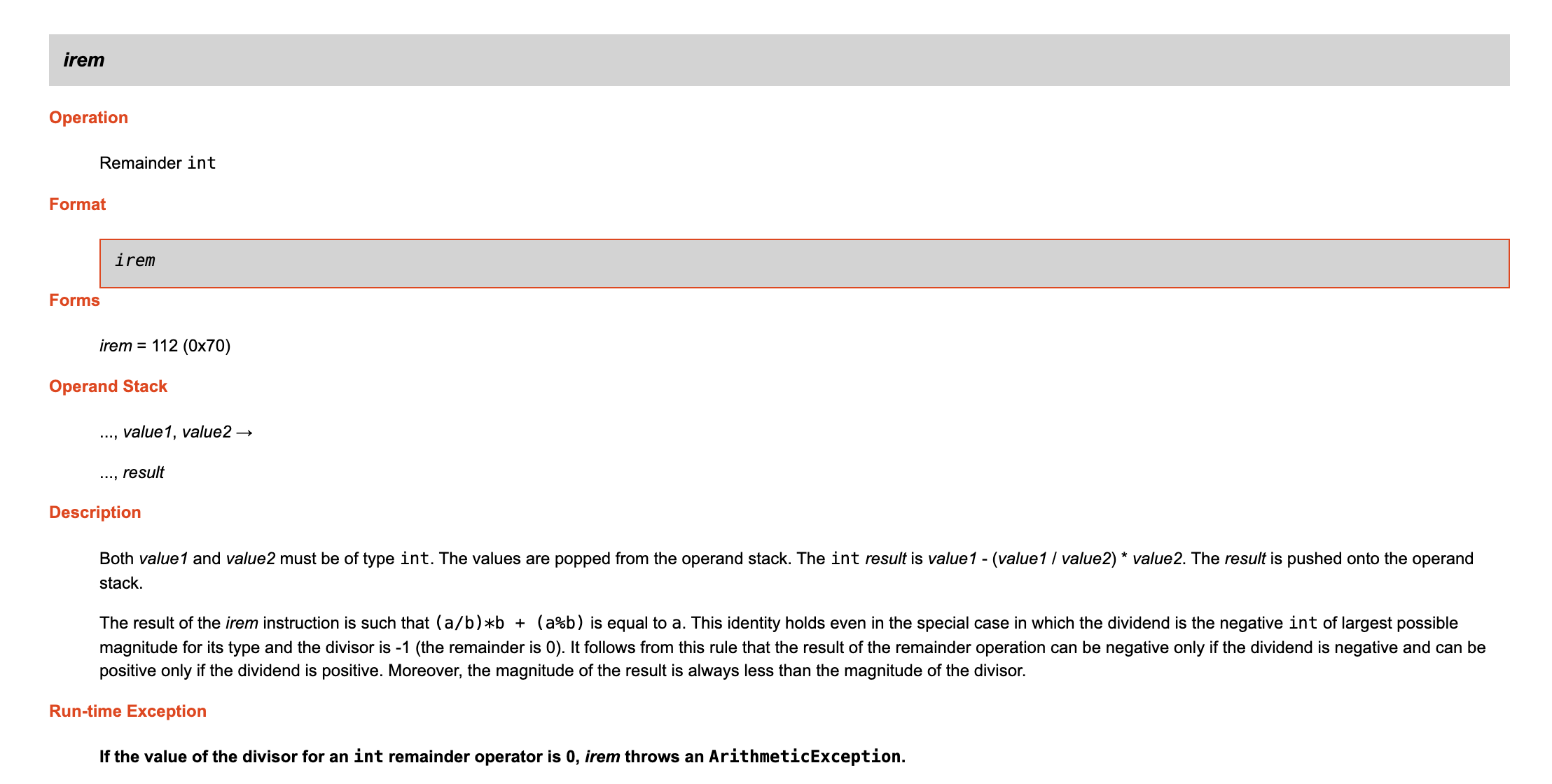
irem定义

为防止图片加载失败，这里贴出其关键部分的描述：

Description
Both value1 and value2 must be of type int. The values are popped from the operand stack. The int result is value1 - (value1 / value2) * value2. The result is pushed onto the operand stack.

The result of the irem instruction is such that (a/b)*b + (a%b) is equal to a. This identity holds even in the special case in which the dividend is the negative int of largest possible magnitude for its type and the divisor is -1 (the remainder is 0). It follows from this rule that the result of the remainder operation can be negative only if the dividend is negative and can be positive only if the dividend is positive. Moreover, the magnitude of the result is always less than the magnitude of the divisor.

Run-time Exception
If the value of the divisor for an int remainder operator is 0, irem throws an ArithmeticException.

这里明确了取模操作（irem）的计算规则，其结果应为 value1 - (value1 / value2) * value2 ，并给出了一些推论及边界条件限制。推论我们先暂且不论，当你乍一看这结果，后面那部分除了再乘不还是 value1 嘛，自己减自己不就 0 了。而事实是，因为 value1 / value2 是整数操作，除完之后直接将小数部分给省略了。

其中提到的推论：

余数的符号是跟着被除数（value1）走的
余数的绝对值小于除数（value2）的绝对值，取值范围为（-value2, value2）
(a / b) * b + (a % b) = a 等式恒成立

让我们回到开始的算式 -9 % 2，对应到 jvm 中拿到的结果就是 -9 - (-4) * 2 ，即 -1。破案了！

接下来再看看 jvm 是怎么执行的，验证一下。因为 jvm 屏蔽了不同架构下字节码的执行细节，因此，需要查看具体架构下，jvm 是怎么解释执行的。以 hotspot 为例，看看 x86 架构下是怎么玩的。在 openjdk 项目（master分支，当前最新提交为[807f6f7]）中找到这样一段代码^[2]：

// templateTable_x86.cpp
void TemplateTable::irem() {
  transition(itos, itos);
  __ movl(rcx, rax);
  __ pop_i(rax);
  // Note: could xor rax and ecx and compare with (-1 ^ min_int). If
  //       they are not equal, one could do a normal division (no correction
  //       needed), which may speed up this implementation for the common case.
  //       (see also JVM spec., p.243 & p.271)
  __ corrected_idivl(rcx);
  __ movl(rax, rdx);
}

其中 movl、pop_i 都是数据搬运操作，从 rax 寄存器搬到 rcx，从栈顶搞了个数到 rax，把 rcx 寄存器的内容传入了 corrected_idivl 操作，最后把 rdx 寄存器的值搬到 rax 寄存器。看上去好像没什么关联，因此，这里需要重点关注下 corrected_idivl，看看到底发生了什么事。我们知道 idiv 系列指令是有符号除法，根据注释，这里的 corrected_idivl 是对于边界情况做了些处理的封装版本。抛开边界情况不论，我们去看看有符号除法的具体实现是怎样的。这里找到一份 Intel 的开发手册^[3]，里面有这样一段描述：

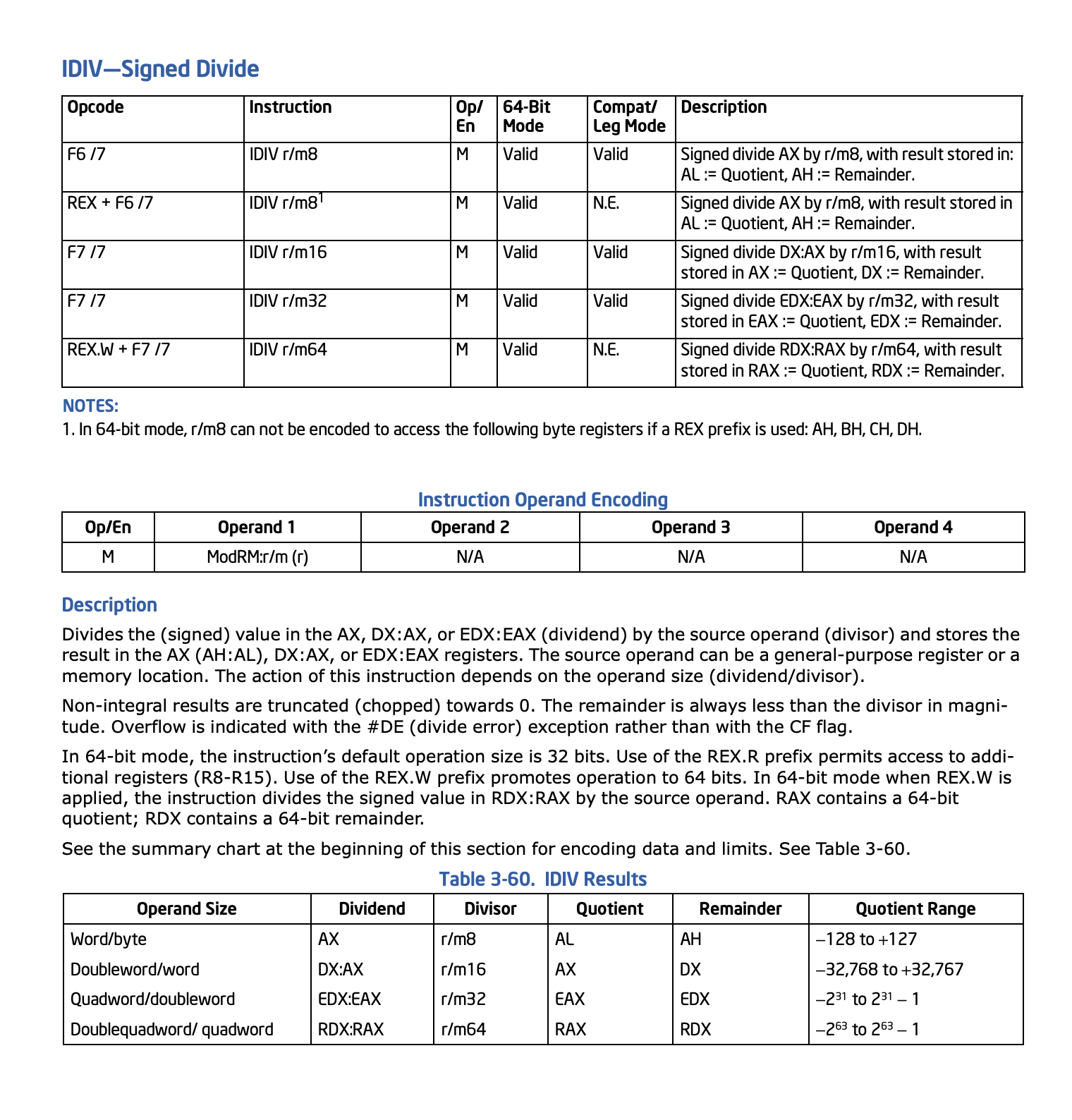
intel开发手册-idiv

从表格中可以看出，rdx 作为高 64 位，rax 作为低 64 位，放在一起作为被除数（value1），而传入的内容作为除数（value2），得到的结果分为商和余数，商放在 rax，余数放在 rdx。这与上面 void TemplateTable::irem() 的行为相符。而实际上，在 64 位机器上，rax 是 64 位寄存器，eax 是其低 32 位，ax 是其低 16 位。rdx、edx、dx 同理。因为 java 中 int 是 32 位无符号整数，因此实际使用到的是 rax 中的 eax 部分进行的运算，idivl 便是其 32 位版本。而在 32 位机器上，并没有 rdx、rax 寄存器，edx、eax 作为独立的寄存器存在。因此这段代码在实际执行之前应该还有一步转换操作，或者还有个 32 位版本。果然，在该项目中又找到了这些代码^{[4] [5]}：

// register_x86.cpp
const char * Register::RegisterImpl::name() const {
  static const char *const names[number_of_registers] = {
#ifdef _LP64
    "rax", "rcx", "rdx", "rbx", "rsp", "rbp", "rsi", "rdi",
    "r8",  "r9",  "r10", "r11", "r12", "r13", "r14", "r15",
    "r16", "r17", "r18", "r19", "r20", "r21", "r22", "r23",
    "r24", "r25", "r26", "r27", "r28", "r29", "r30", "r31"
#else
    "eax", "ecx", "edx", "ebx", "esp", "ebp", "esi", "edi"
#endif // _LP64
  };
  return is_valid() ? names[encoding()] : "noreg";
}

// register_x86.hpp
constexpr Register rax = as_Register(0);
constexpr Register rcx = as_Register(1);
constexpr Register rdx = as_Register(2);
constexpr Register rbx = as_Register(3);
constexpr Register rsp = as_Register(4);
constexpr Register rbp = as_Register(5);
constexpr Register rsi = as_Register(6);
constexpr Register rdi = as_Register(7);
#ifdef _LP64
constexpr Register r8  = as_Register( 8);
constexpr Register r9  = as_Register( 9);
constexpr Register r10 = as_Register(10);
constexpr Register r11 = as_Register(11);
constexpr Register r12 = as_Register(12);
constexpr Register r13 = as_Register(13);
constexpr Register r14 = as_Register(14);
constexpr Register r15 = as_Register(15);
constexpr Register r16 = as_Register(16);
constexpr Register r17 = as_Register(17);
constexpr Register r18 = as_Register(18);
constexpr Register r19 = as_Register(19);
constexpr Register r20 = as_Register(20);
constexpr Register r21 = as_Register(21);
constexpr Register r22 = as_Register(22);
constexpr Register r23 = as_Register(23);
constexpr Register r24 = as_Register(24);
constexpr Register r25 = as_Register(25);
constexpr Register r26 = as_Register(26);
constexpr Register r27 = as_Register(27);
constexpr Register r28 = as_Register(28);
constexpr Register r29 = as_Register(29);
constexpr Register r30 = as_Register(30);
constexpr Register r31 = as_Register(31);
#endif // _LP64

看起来是选择了前者，能对应上的便通过编号对应上，对应不上的就拉倒，蛮好，上层就不需要一套逻辑写几遍了。

在手册中，其中还有一段描述值得注意：Non-integral results are truncated (chopped) towards 0. 即商不是整数的时候，结果会向 0 截断，也就是舍弃小数部分（无论正负，舍弃掉小数部分后都离 0 更近）。

再往下就是汇编在具体平台上变成机器码，然后控制器和运算器怎么配合，指令怎么搬运到指令寄存器，数据怎么搬运到数据寄存器，时钟怎么调度，流水线怎么设计，总线怎么仲裁，微指令还是硬连线，mips 还是 cips，有哪些状态寄存器，指令长度如何，每一位都是什么操作balabala 就没必要细究了。每个硬件平台有着不同的设计，这是 jvm 需要操心的事情，他们会有他们之间的承诺和约定。对于取模操作这个问题，我们只需要关心 jvm 给了我们什么样的承诺即可。

那 python 是怎么回事

既然硬件都已经给算好了结果，放寄存器里了（虽然不是所有的都会这么干），python 为什么不直接拿出来做返回值呢（java 就是这么做的），反而自己再去搞一套玩法再实现一遍。难道还有另外一套规范？我在维基百科上找到了答案 ^[6]。

还记得我们在 jvm 规范中看到的描述吗，irem 的结果为value1 - (value1 / value2) * value2。我们说这个式子最后没有变成 value1 - value1 = 0 是因为 value1 / value2 除不尽，舍弃了小数部分，于是得到了最终的结果。乍一看挺合理的，但是在看完了维基百科的介绍之后，原来各家在商的取整上还是有分歧的。反倒是取模的结果是value1 - (value1 / value2) * value2这个定义上并没有表现出什么分歧。可以来看看都有哪些流派，以下这些流派说的是对于 value1 / value2 进行取整的各个主张。

截断式

就是 java、JavaScript 这种的，小数部分直接扔了。也即(value1 / value2) > 0 的时候向下取整，(value1 / value2) < 0 的时候向上取整，等于 0 就是 0。

向下取整式

不管正负，运算结果向下取整。python 小兄弟用的这种！！！

欧几里得式

value2 > 0 的时候向下取整，value2 < 0 的时候向上取整，别问等于 0 怎么办，等于 0 修 bug好吧。

四舍五入式

字面意思，运算结果四舍五入，离谁近跟谁。

向上取整式

不管正负，运算结果向上取整。

其中还列出了各个流派商和余数取值范围和分布情况，以及各个语言在进行取模操作的时候，遵循的是哪个流派，不少编程语言支持使用不同的语法选取不同的流派，感兴趣的朋友可以参考一下。

既然分歧不在余数而在商！那么 python 除法真的是向下取整吗？注意，python 的整数除法是双斜杠，单斜杠除出来是浮点数。

❯ python                                                                   
Python 3.11.5 (main, Sep 11 2023, 08:19:27) [Clang 14.0.6 ] on darwin
Type "help", "copyright", "credits" or "license" for more information.
>>> -9 / 2
-4.5
>>> -9 // 2
-5

还真是！好嘛，除法也要当心了哈哈。祝大家写不出 bug。

[1] https://docs.oracle.com/javase/specs/jvms/se8/html/jvms-6.html#jvms-6.5.irem

[2] https://github.com/openjdk/jdk/blob/master/src/hotspot/cpu/x86/templateTable_x86.cpp

[3] https://cdrdv2-public.intel.com/843820/325462-sdm-vol-1-2abcd-3abcd-4-1.pdf

[4] https://github.com/openjdk/jdk/blob/master/src/hotspot/cpu/x86/register_x86.cpp

[5] https://github.com/openjdk/jdk/blob/master/src/hotspot/cpu/x86/register_x86.hpp

[6] https://en.wikipedia.org/wiki/Modulo

打赏-支付宝